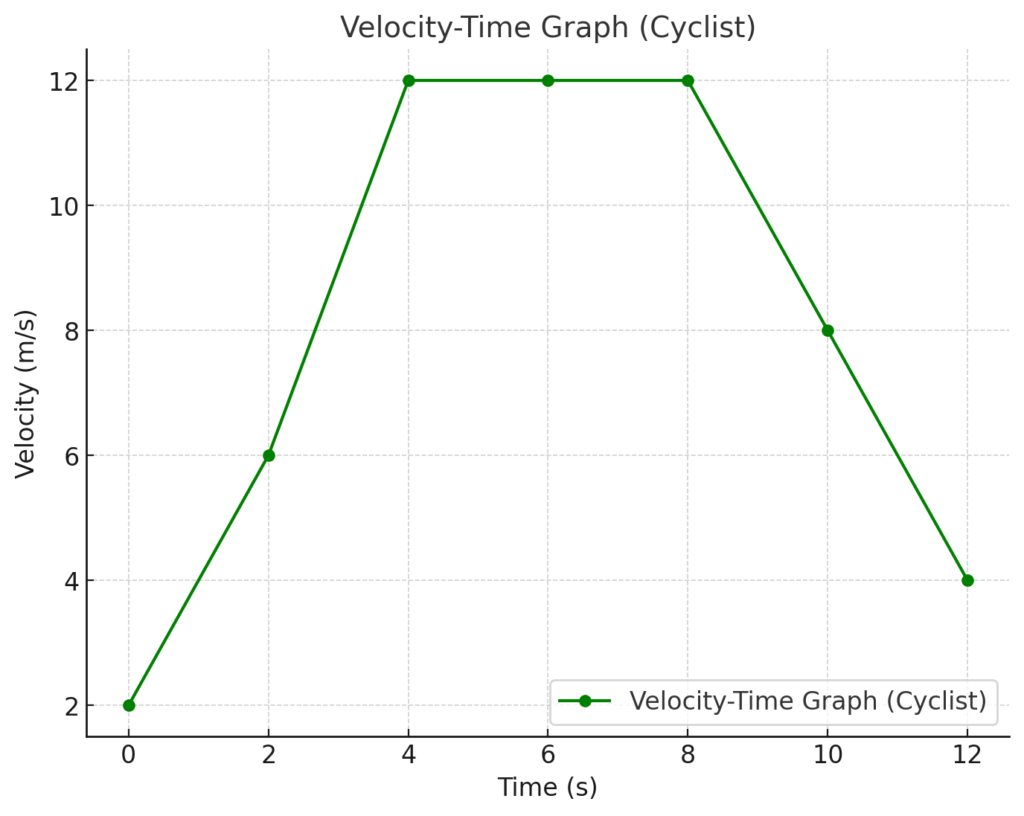
Velocity-Time Graph Question 2
The graph below shows the motion of a cyclist over a period of 12 seconds.
Graph Description:
- The cyclist starts at a velocity of 2 m/s and accelerates uniformly to 12 m/s in the first 4 seconds.
- From 4 seconds to 8 seconds, the cyclist maintains a constant velocity of 12 m/s.
- From 8 seconds to 12 seconds, the cyclist decelerates uniformly to a velocity of 4 m/s.
Graph Data Points:
- Time (s): 0, 2, 4, 6, 8, 10, 12
- Velocity (m/s): 2, 6, 12, 12, 12, 8, 4
1. Sketch the velocity-time graph based on the description provided.
The velocity-time graph is already plotted based on the given data points and description.
2. For how long does the cyclist travel at a constant velocity?
From the graph:
- The cyclist maintains a constant velocity of 12 m/s from t = 4 s to t = 8 s.
The cyclist travels at a constant velocity for 4 seconds.
3. What is the acceleration of the cyclist during the first 4 seconds?
The formula for acceleration is:
a = (Δv) / (Δt)
- Initial velocity (u) = 2 m/s
- Final velocity (v) = 12 m/s
- Time (t) = 4 s
Substituting values:
a = (12 – 2) / 4 = 10 / 4 = 2.5 m/s2
The acceleration is 2.5 m/s2.
4. What is the deceleration of the cyclist from 8 seconds to 12 seconds?
The formula for deceleration is:
a = (Δv) / (Δt)
- Initial velocity (u) = 12 m/s
- Final velocity (v) = 4 m/s
- Time (t) = 12 – 8 = 4 s
Substituting values:
a = (4 – 12) / 4 = -8 / 4 = -2 m/s2
The deceleration is 2 m/s2.
5. Calculate the total distance traveled by the cyclist during the 12 seconds.
The total distance is the area under the velocity-time graph, divided into three regions:
Region 1 (Acceleration phase: 0 to 4 seconds):
Area = Area of a trapezium
Area = 1/2 × (2 + 12) × 4 = 28 m
Region 2 (Constant velocity phase: 4 to 8 seconds):
Area = Area of a rectangle
Area = 4 × 12 = 48 m
Region 3 (Deceleration phase: 8 to 12 seconds):
Area = Area of a trapezium
Area = 1/2 × (12 + 4) × 4 = 32 m
Total distance = 28 + 48 + 32 = 108 m
The total distance traveled by the cyclist is 108 m.