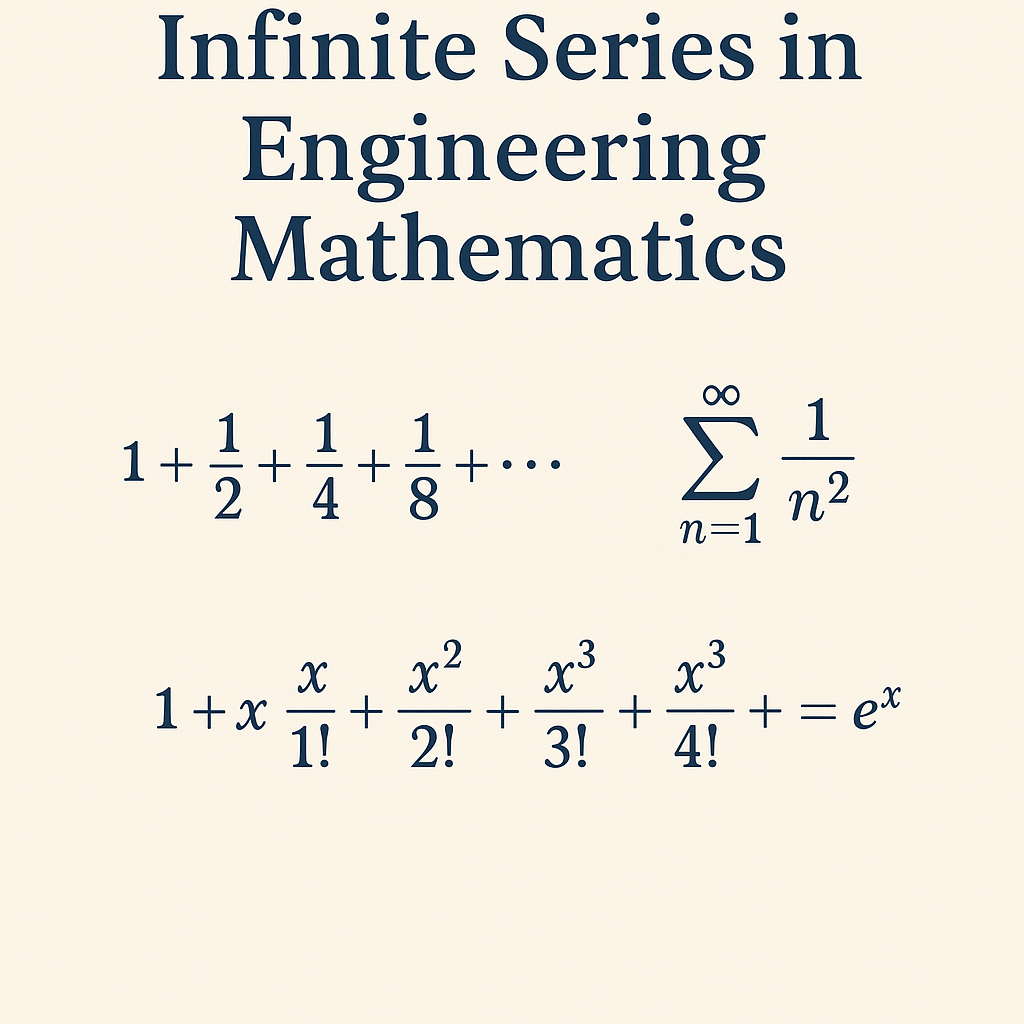Understanding Infinite Series in Engineering Mathematics
Infinite series play a fundamental role in engineering mathematics, enabling engineers and scientists to approximate functions, solve differential equations, and model physical phenomena. This article delves into the concept of infinite series, explaining their types, convergence criteria, and applications in engineering contexts.
What is an Infinite Series?
An infinite series is the sum of the terms of an infinite sequence. Mathematically, if an represents the terms of a sequence, then the infinite series is written as:
S = a1 + a2 + a3 + … + an + …
Convergence and Divergence
The behavior of an infinite series is determined by whether it converges or diverges:
- Convergent Series: The series approaches a finite limit as the number of terms goes to infinity.
- Divergent Series: The series increases without bound or oscillates as more terms are added.
The sum S of a convergent series is defined as:
\( S = \lim_{n \to \infty} \sum_{k=1}^{n} a_k \)
Types of Infinite Series
Several important types of infinite series are widely used in engineering:
1. Geometric Series
A geometric series has a constant ratio between successive terms. It is of the form:
a + ar + ar2 + ar3 + …
This series converges if |r| < 1, and the sum is:
S = a / (1 – r)
2. Harmonic Series
The harmonic series is:
1 + 1/2 + 1/3 + 1/4 + …
It diverges, even though the terms decrease.
3. p-Series
A p-series has the form:
\( \sum_{n=1}^{\infty} \frac{1}{n^p} \)
It converges if p > 1 and diverges if p ≤ 1.
Tests for Convergence
Various tests help determine whether a series converges:
- Ratio Test: Evaluates the limit of the ratio of successive terms.
- Root Test: Involves the n-th root of the absolute value of terms.
- Integral Test: Compares a series with an integral.
- Comparison Test: Compares a series with a known convergent or divergent series.
Applications in Engineering
Infinite series are used in multiple engineering applications, such as:
- Signal Processing: Fourier series represent periodic signals as sums of sine and cosine terms.
- Control Systems: Laplace transforms often involve power series for system analysis.
- Structural Analysis: Deflection of beams and stress analysis use series solutions.
- Heat Transfer: Series solutions to the heat equation describe temperature distribution.
Conclusion
Infinite series form a cornerstone of mathematical modeling in engineering. From Fourier transforms to solving differential equations, the ability to analyze and utilize infinite series allows engineers to design and predict system behaviors with accuracy. Understanding convergence and applying the right type of series can simplify complex engineering problems significantly.